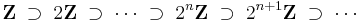Integral domain
In abstract algebra, an integral domain is a commutative ring that has no zero divisors,[1] and which is not the trivial ring {0}. It is usually assumed that commutative rings and integral domains have a multiplicative identity even though this is not always included in the definition of a ring. Integral domains are generalizations of the integers and provide a natural setting for studying divisibility. An integral domain is a commutative domain with identity.[2]
The above is how "integral domain" is almost universally defined, but there is some variation. In particular, noncommutative integral domains are sometimes admitted.[3] However, we follow the much more usual convention of reserving the term integral domain for the commutative case and use domain for the noncommutative case; this implies that, curiously, the adjective "integral" means "commutative" in this context. Some sources, notably Lang, use the term entire ring for integral domain.[4]
Some specific kinds of integral domains are given with the following chain of class inclusions:
- Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields
The absence of zero divisors means that in an integral domain the cancellation property holds for multiplication by any nonzero element a: an equality ab = ac implies b = c.
Contents |
Definitions
There are a number of equivalent definitions of integral domain:
- An integral domain is a commutative ring with identity in which for any two elements a and b, the equality ab = 0 implies either a = 0 or b = 0.
- An integral domain is a commutative ring with identity in which the zero ideal {0} is a prime ideal.
- An integral domain is a commutative ring with identity that is a subring of a field.
- An integral domain is a commutative ring with identity in which for every non-zero element r, the function that maps every element x of the ring to the product xr is injective. Elements that have this property are called regular, so it is equivalent to require that every non-zero element of the ring be regular.
Examples
- The prototypical example is the ring Z of all integers.
- Every field is an integral domain. Conversely, every Artinian integral domain is a field. In particular, all finite integral domains are finite fields (more generally, by Wedderburn's little theorem, finite domains are finite fields). The ring of integers Z provides an example of a non-Artinian infinite integral domain that is not a field, possessing infinite descending sequences of ideals such as:
- Rings of polynomials are integral domains if the coefficients come from an integral domain. For instance, the ring Z[X] of all polynomials in one variable with integer coefficients is an integral domain; so is the ring R[X,Y] of all polynomials in two variables with real coefficients.
- For each integer n > 1, the set of all real numbers of the form a + b√n with a and b integers is a subring of R and hence an integral domain.
- For each integer n > 0 the set of all complex numbers of the form a + bi√n with a and b integers is a subring of C and hence an integral domain. In the case n = 1 this integral domain is called the Gaussian integers.
- The p-adic integers.
- If U is a connected open subset of the complex number plane C, then the ring H(U) consisting of all holomorphic functions f : U → C is an integral domain. The same is true for rings of analytic functions on connected open subsets of analytic manifolds.
- If R is a commutative ring and P is an ideal in R, then the factor ring R/P is an integral domain if and only if P is a prime ideal. Also, R is an integral domain if and only if the ideal (0) is a prime ideal.
- A regular local ring is an integral domain. In fact, a regular local ring is a UFD.[5][6]
The following rings are not integral domains.
- The ring of n×n matrices over any non-trivial ring when n ≥ 2.
- The ring of continuous functions on the unit interval.
- The quotient ring Z/m when m is a composite number.
- The commutative ring with a multiplicative identity Z×Z.
Divisibility, prime and irreducible elements
If a and b are elements of the integral domain R, we say that a divides b or a is a divisor of b or b is a multiple of a if and only if there exists an element x in R such that ax = b.
The elements which divide 1 are called the units of R; these are precisely the invertible elements in R. Units divide all other elements.
If a divides b and b divides a, then we say a and b are associated elements or associates.
If q is a non-unit, we say that q is an irreducible element if q cannot be written as a product of two non-units.
If p is a non-zero non-unit, we say that p is a prime element if, whenever p divides a product ab, then p divides a or p divides b. Equivalent, an element is prime if and only if an ideal generated by it is a nonzero prime ideal. Every prime element is irreducible. Conversely, in a GCD domain (e.g., a unique factorization domain), an irreducible element is a prime element.
The notion of prime element generalizes the ordinary definition of prime number in the ring Z, except that it allows for negative prime elements. While every prime is irreducible, the converse is not in general true. For example, in the quadratic integer ring ![\mathbb{Z}\left[\sqrt{-5}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/33dc21bfb7dd49a2520264f0e6595cc6.png) the number 3 is irreducible, but is not a prime because 9, the norm of 3, can be factored in two ways in the ring, namely,
the number 3 is irreducible, but is not a prime because 9, the norm of 3, can be factored in two ways in the ring, namely, 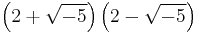 and
and 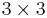 . Thus
. Thus 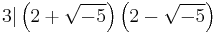 , but 3 does not divide
, but 3 does not divide 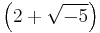 nor
nor 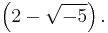 The numbers 3 and
The numbers 3 and 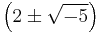 are irreducible as there is no
are irreducible as there is no 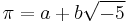 where
where 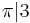 or
or 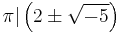 as
as 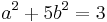 has no integer solution.
has no integer solution.
While unique factorization does not hold in the above example, if we use ideals we do get unique factorization. Namely, the ideal 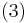 equals the ideals
equals the ideals 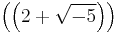 and
and 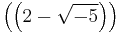 and is the unique product of the two prime ideals:
and is the unique product of the two prime ideals: 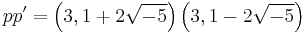 , each of which have a norm of 3.
, each of which have a norm of 3.
Properties
- Let R be an integral domain. Then there is an integral domain S such that R ⊂ S and S has an element which is transcendental over R.
- The cancellation property holds in integral domains. That is, let a, b, and c belong to an integral domain. If a ≠ 0 and ab = ac then b = c. Another way to state this is that the function x ↦ ax is injective for any non-zero a in the domain.
- An integral domain is equal to the intersection of its localizations at maximal ideals.
Field of fractions
If R is a given integral domain, the smallest field containing R as a subring is uniquely determined up to isomorphism and is called the field of fractions or quotient field of R. It can be thought of as consisting of all fractions a/b with a and b in R and b ≠ 0, modulo an appropriate equivalence relation. The field of fractions of the integers is the field of rational numbers. The field of fractions of a field is isomorphic to the field itself.
Algebraic geometry
In algebraic geometry, integral domains correspond to irreducible varieties. They have a unique generic point, given by the zero ideal. Integral domains are also characterized by the condition that they are reduced and irreducible. The former condition ensures that the nilradical of the ring is zero, so that the intersection of all the ring's minimal primes is zero. The latter condition is that the ring have only one minimal prime. It follows that the unique minimal prime ideal of a reduced and irreducible ring is the zero ideal, hence such rings are integral domains. The converse is clear: No integral domain can have nilpotent elements, and the zero ideal is the unique minimal prime ideal.
Characteristic and homomorphisms
The characteristic of every integral domain is either zero or a prime number.
If R is an integral domain with prime characteristic p, then f(x) = x p defines an injective ring homomorphism f : R → R, the Frobenius endomorphism.
See also
- Integral domains – wikibook link
- Dedekind–Hasse norm – the extra structure needed for an integral domain to be principal
- Zero-product property
Notes
- ^ Dummit and Foote, p. 229
- ^ Rowen (1994), p. 99 at Google Books.
- ^ J.C. McConnel and J.C. Robson "Noncommutative Noetherian Rings" (Graduate studies in Mathematics Vol. 30, AMS)
- ^ Pages 91–92 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0
- ^ Maurice Auslander; D.A. Buchsbaum (1959). "Unique factorization in regular local rings". Proc. Natl. Acad. Sci. USA 45 (5): 733–734. doi:10.1073/pnas.45.5.733. PMC 222624. PMID 16590434. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=222624.
- ^ Masayoshi Nagata (1958). "A general theory of algebraic geometry over Dedekind domains. II". Amer. J. Math. (The Johns Hopkins University Press) 80 (2): 382–420. doi:10.2307/2372791. JSTOR 2372791.
References
- Iain T. Adamson (1972). Elementary rings and modules. University Mathematical Texts. Oliver and Boyd. ISBN 0-05-002192-3.
- Bourbaki, Nicolas (1988). Algebra. Berlin, New York: Springer-Verlag. ISBN 978-3-540-19373-9.
- Mac Lane, Saunders; Birkhoff, Garrett (1967). Algebra. New York: The Macmillan Co.. ISBN 1568810687. MR0214415.
- Dummit, David S.; Foote, Richard M. (1999). Abstract algebra (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-471-36857-1.
- Hungerford, Thomas W. (1974). Algebra. New York: Holt, Rinehart and Winston, Inc.. ISBN 0030305586.
- Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. 211. Berlin, New York: Springer-Verlag. ISBN 978-0-387-95385-4. MR1878556.
- David Sharpe (1987). Rings and factorization. Cambridge University Press. ISBN 0-521-33718-6.
- Louis Halle Rowen (1994). Algebra: groups, rings, and fields. A K Peters. ISBN 1568810288.
- Charles Lanski (2005). Concepts in abstract algebra. AMS Bookstore. ISBN 053442323X.
- César Polcino Milies; Sudarshan K. Sehgal (2002). An introduction to group rings. Springer. ISBN 1402002386.